“天河”系列超级计算机应用成果报道--高效网格变形技术研究

---

网格变形技术是动网格技术的一种，变形前后网格拓扑保持不变，被广泛应用于流固耦合仿真、航天航空飞行器气动外形优化设计等领域。

在众多的网格变形方法中，径向基函数法（Radial Basis Functions，RBF）由于不依赖网格拓扑，具有广泛的适用性，且鲁棒性好，能够处理大变形，并保证变形后的网格具有较高质量，尤其是能够很好的保留近壁网格的正交性，因而逐渐成为研究热点。

然而，RBF方法计算量十分巨大。对此，研究者提出了众多改进算法，例如贪心算法、多级子空间法、峰值选点法、多尺度法等。这些算法虽然在一定程度上提高了基于RBF的网格变形效率，但若应用于复杂、大规模、非稳态流固耦合仿真中，其计算效率依然是重大制约因素。

针对这一问题，北京临近空间飞行器系统工程研究所方洪（第一作者）提出了Cholesky分解法和笛卡尔背景网格法等高效算法，相关成果已发表在计算流体力学顶刊Journal of Computational Physics上。

近期，方洪（第一作者）与单繁立（通讯作者）又在国际上首次提出了分组循环贪心算法(Grouping-Circular-Based greedy algorithm)，并依托天河系列超级计算机进行了算法测试，将网格变形效率提高了1个数量级，使得网格变形不再是流固耦合仿真的计算瓶颈，相关成果再次发表在计算流体力学顶刊JCP上。

应用成果

贪心算法是一种RBF支撑点精简算法，能够提高网格变形效率。传统贪心算法在每次迭代时均要计算所有边界点的插值误差，并将最大插值误差点加入支撑点集合。这部分计算量占整个网格变形的85%以上。由于贪心算法是寻找一个较小的支撑点集合以取代原始支撑点集合，并确保插值精度得到满足，本质上是一种逐次逼近算法，因此在不影响插值精度的前提下，如果只将插值误差足够大的点加入支撑点集合，亦可达到逐次逼近的效果。虽然其代价是支撑点集合稍有增大，但计算效率可以得到显著提升。

基于这一创新概念，方洪与单繁立提出了分组循环贪心算法，该算法不再从所有边界点中搜索最大插值误差点，而是将边界点随机分为m组，用每组最大插值误差作为全局最大插值误差的近似，并在理论上证明了所产生的支撑点集合的合理性以及具有与原始支撑点集合一致的统计特性。运用这一算法，支撑点精简过程的计算复杂度可由O (N2 cNb)降低至O (Nc3)（Nb和N c分别表示边界点与支撑点的数量）。对于典型分组情况，支撑点精简效率可大幅提升至原先的数十倍。

分组循环贪心算法是对传统贪心算法的重大改进，其理论与实践意义与多重网格之于加速收敛类似。基于该算法，团队开发了相应的网格变形计算软件，并在DLR-F6组合体（图1）变形问题中对算法性能进行了验证与研究。结果显示，支撑点精简过程所用时间由传统贪心算法的729.84秒减少到26.78秒（图2），效率提高27.25倍，网格总体变形效率提高9.8倍。图3和图4分别展示了运用该算法得到的支撑点分布以及变形后的网格分布。

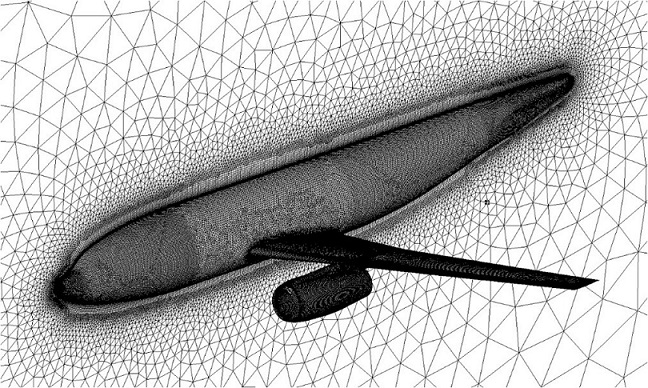
图1  DLR-F6组合体原始网格

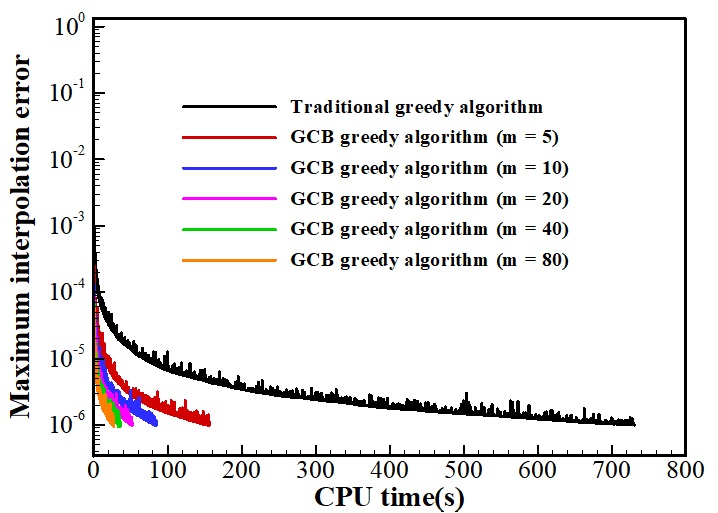
图2  分组循环贪心算法与传统贪心算法的效率对比

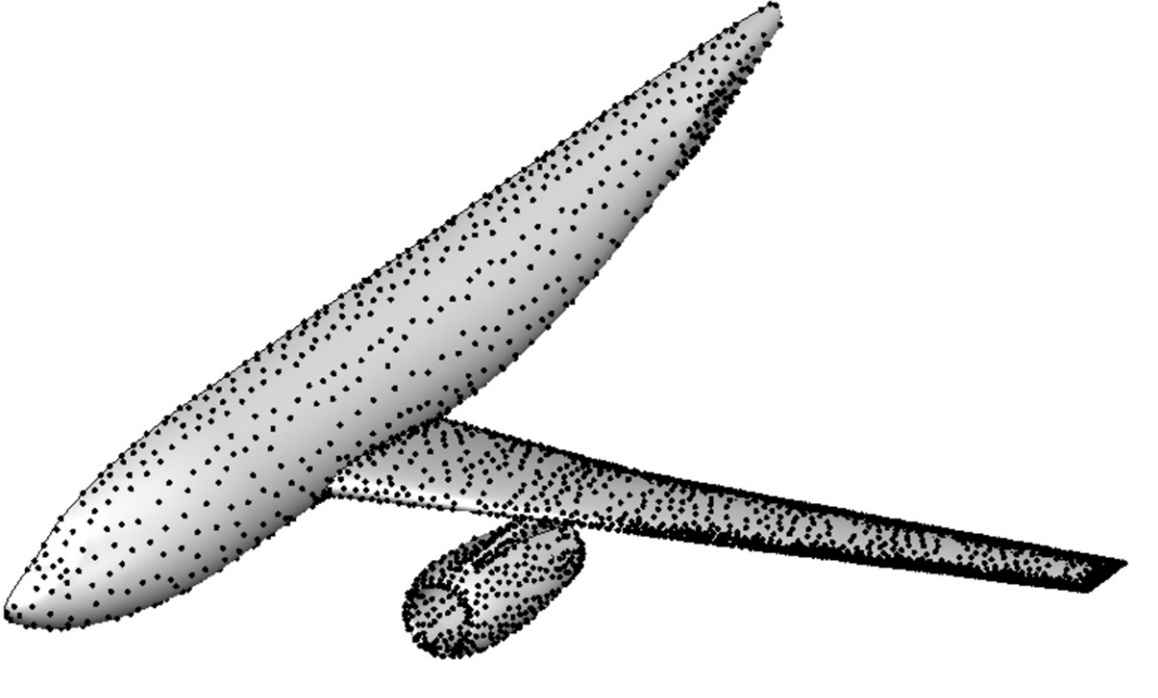
图3  DLR-F6组合体支撑点分布

图4  DLR-F6组合体变形后网格

上述研究工作得到了科技部重点研发计划“高端装备复杂流场自主CAE一体化平台”项目支持，相关测试、调优、计算等工作得到了国家超级计算天津中心的大力支持。