
应用领域介绍:
基础科学研究是指认识自然现象、揭示自然规律,获取新知识、新原理、新方法的研究活动。加强基础研究是提高我国原始创新能力、积累智力资本的重要途径,是跻身世界科技强国的必要条件,是建设创新型国家的根本动力和源泉。
国家超级计算天津中心与中科院软件所、中科院力学研究所、中科院药物所、中科院计算数学所、国家计算流体力学等多家单位合作,在新能源、新材料、凝聚态物理、粒子液体模拟、天文观察、碳纳米材料储氢机制研究等基础科学领域进行研究,为我国基础科学的发展助力。
解决方案与服务内容:
可提供基础科学研究领域中的各类数值模拟服务,中心工作人员可协助用户配置作业脚本,设置若干可能影响计算性能的参数,完成相关计算模拟任务,并协助用户分析应用程序热点和提出优化建议。
凝聚态物理领域
领域介绍
强关联凝聚态物理系统涵盖了金属绝缘体莫特转变,量子相变附近的非费米液体,非常规超导体(铜基、铁基),以拓扑绝缘体为代表的拓扑物质形态,低维磁性系统中量子相变,量子自旋液体和量子自旋冰,以石墨烯为代表的新材料等等领域。了解它们的性质是凝聚态物理学研究的主要课题,但是由于这些系统往往极具复杂,展现出非微扰、强关联的量子多体效应,解析的方法无法提供定量的结果。在这样的情况下,以大尺度量子蒙特卡洛模拟(Quantum Monte Carlo simulation (QMC))为代表的无偏差或少偏差的数值模拟方法,随着计算机性能的突飞猛进,在这些艰深的课题上体现出了力量,帮助人们扩展对强关联的凝聚态物理系统的认识。
典型案例:
中科院物理所T03团队从事强关联电子系统的大尺度量子蒙特卡洛模拟研究,探索这些系统中涌现出的新奇量子相变和量子态。在研究工作方面得到了国家超算天津中心的大力支持。
(一)相互作用的拓扑物质形态。拓扑物态,如具有拓扑序的量子霍尔态以及拓扑绝缘体,是近年来凝聚态物理领域最大的进展之一。在拓扑绝缘体中加入电子之间的强关联相互作用,研究可能涌现的新的拓扑物态,以及拓扑物态之间由于相互作用驱动的拓扑相变,是人们关心的问题。该团队运用费米子量子蒙特卡洛方法:(1)发现相互作用下的拓扑相变,第一次指出强关联电子系统的拓扑相变不能用单粒子格林函数构造的陈数来描述,而是需要在集体激发中寻找体系的拓扑信息。(2)发现第一个可以用量子蒙特卡洛严格计算的,从相互作用费米子系统中涌现的bosonic symmetry protected topological (SPT) phase微观模型,为研究具有短程纠缠的拓扑物态及其量子相变铺平了道路,该模型所具有的SO(4)+Theta-term 量子相变与近年来在量子磁性系统中发现的去禁闭量子临界点具有深层联系。(3)提出了一种针对弱耦合区域相互作用导致的拓扑物态的通用诊断方案,利用严格对角化方法给出的本征值及本征波函数,结合点群操作算符的本征值和关联函数信息,分析出体系热力学极限的序参量对称性和基态可能的拓扑数。根据这一方案,第一次从数值上给出了棋盘格子上具有最近邻排斥相互作用的无自旋费米子模型中存在由相互作用导致的陈绝缘体。
(二)阻挫磁体和量子自旋液体。量子自旋液体是凝聚态物理理论研究中难点与突破点,这种由于量子临界涨落和磁阻挫的结合在量子磁性系统中涌现出的奇异物质形态,反复出现在凝聚态物理研究的各个方向。该团队运用玻色子量子蒙特卡洛模拟方法(1)确定硬壳玻色子在烧绿石晶格上的基态相图,发现了其中量子自旋冰相,以及量子自旋冰中满足量子电动力学规范场理论描述的低能“光子”激发。为量子自旋冰材料合成,中子、RIXS散射、核磁共振实验探测提供理论指导。(2)确定三维反铁磁 Heisenberg模型从磁有序态到二聚化磁无序态的量子临界行为,验证了上临界维度处的相变对数修正,发现量子临界点附近的希格斯玻色子振幅模(Higgs mode),为二聚反铁磁体量子临界点附近的中子、RIXS散射实验探测提供理论依据。
中国科学院物理研究所/北京凝聚态物理国家实验室(筹)与安徽师范大学、复旦大学、中国科技大学组成的研究团队,运用量子蒙特卡洛蠕虫算法,使用“天河一号”超级计算机和其他计算平台,研究了三维阻挫磁体中可能存在的量子自旋冰和团簇莫特绝缘体。通过运用大规模量子蒙特卡洛并行计算,第一次完整地给出了硬壳玻色子在pyrochlore lattice 上,以玻色子占据数和相互作用强度为轴的二维相空间中的相图,发现了1/4 和3/4 玻色子占据的两种团簇莫特绝缘体,证实了1/4, 1/2和3/4 玻色子占据的团簇莫特绝缘体(其中1/2 玻色子占据的团簇莫特绝缘体就是量子自旋冰)是具有量子电动力学层展U(1) 规范场特性的奇异物质形态;而且,通过比热和电场关联函数的综合测量直接观测到团簇莫特绝缘体中的层展U(1)规范场。研究团队预计很多阻挫磁体材料都可能是团簇莫特绝缘体,而且接下来与物理所和国内现有的材料合成、中子散射、RIXS 散射等实验团队进行合作,填补国内在阻挫磁体(量子自旋液体、量子自旋冰、团簇莫特绝缘体)这些方面的空白,尽快在世界发展前沿中占有一席之地奠定了基础。
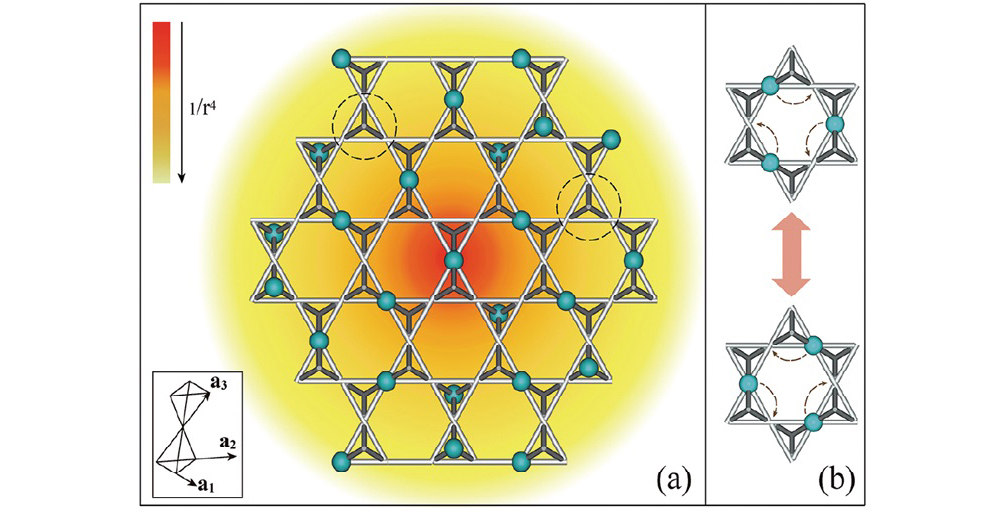
Fig.1.(a)(示意图)1/4 玻色子占据的团簇莫特绝缘体(b)(示意图)团簇莫特绝缘体中的无能隙激发
(三)发展费米子量子蒙特卡洛方法,研究巡游电子系统中的量子临界点。对于巡游电子系统中的量子临界行为的定量描述,如重费米子系统中的磁性量子临界点、铁基超导体中的磁性和nematic量子临界点,是理论凝聚态物理学几十年来的大问题,其难点在于,在临界点附近,无穷多的玻色子临界模和费米面耦合,微扰论和重正化群中的各种展开技巧和准粒子假设对于这样的问题纷纷失效,无法给出定量甚至定性的结果。研究团队正在发展新型的费米子量子蒙特卡洛方法,这种方法赋予传统的行列式蒙特卡洛中的玻色子辅助场新的物理意义,在玻色子辅助场中引入量子临界点,并将临界玻色子辅助场和费米面耦合起来。并发展了自学习蒙特卡洛模拟方法,赋予传统的行列式蒙特卡洛中的玻色子辅助场新的物理意义,优化接收概率,提高算法效率,将强关联费米子模型(如Hubbard模型)的系统尺度从传统的20x20提高到100x100,在领域内引起反响。前期已经取得了有益的结果,研究二维狄拉克半金属中的量子临界点,发现狄拉克半金属在临界点上形成nodal line。研究二维巡游铁磁系统中的量子临界点,第一次严格的发现了量子临界点上的非费米液体行为。
(四)团队证实了相互作用费米子拓扑相变点与解禁闭量子临界点满足对偶变换关系。这既让人们对于相互作用的拓扑相变点和解禁闭量子临界点有了更深刻的认识,更为对偶变换之网的进一步发展,比如拓扑序和量子自旋液体中存在的其他更加高级的对偶变换,给出了有力的支撑。系列研究成果发表在最近一期的Physical Review X期刊。
研究所需的大规模并行计算大部分工作在国家超级计算天津中心的业务主机“天河一号”超级计算机上完成,并得到了天津超算中心工作人员的有力配合:一方面帮助进行计算程序的优化,使得更大晶格的计算变得可行;另一方面,在天河一号系统升级计算资源紧张的情况下,通过合理动态调配节点,使得总计7200核的大规模并行蒙特卡洛计算得以顺利完成。从这项工作还看到,目前国内的超算平台,除了在浮点运算能力上领先世界之外,这些平台实质性地助力基础科学研究的时机已然到来,基础科学研究单位和国家超算中心更加精彩的合作,将会不断涌现
计算化学领域:金团簇
领域介绍
“八电子规则”是现代化学的理论基础,是理解和解释主族元素分子结构稳定性和物化性质的基石。随后发展的“十八电子规则”和“Wade规则”在20世纪也取得巨大成功,成为理解过渡金属分子和小尺寸团簇的基本化学理论。但随着近20年来纳米技术的巨大进展,传统化学理论是否在纳米尺度仍然适用引起人们广泛关注。特别对于金属纳米团簇,迄今人们普遍认为其是由一个一个金属原子随机生长而来,并不存在一个普适的化学规则。
典型案例
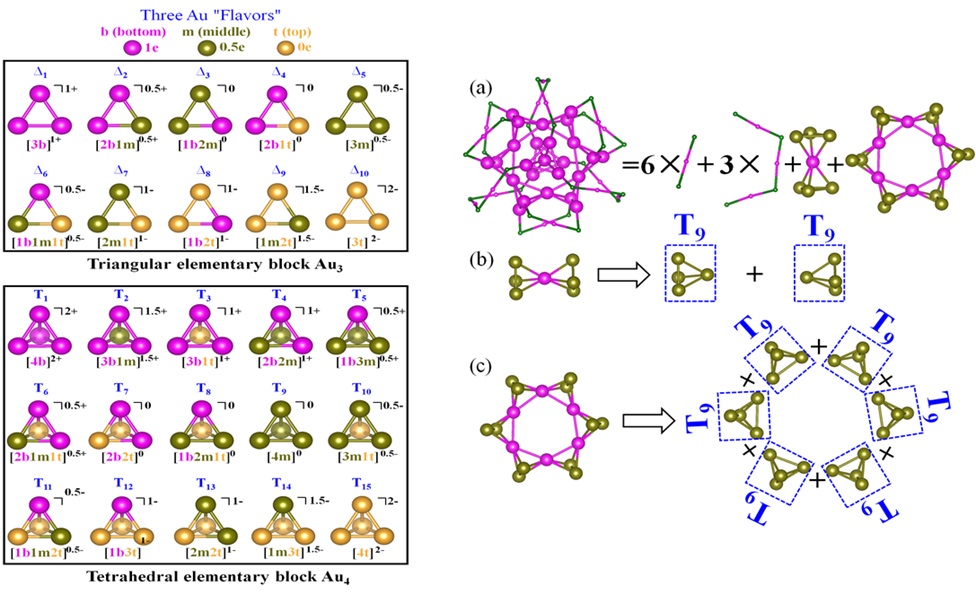
长期以来,配体金纳米团簇因其独特的结构和物理化学性质以及在催化、纳米技术及生物医学等领域广泛的应用前景得到了广泛关注。近10年来,随着一系列大尺寸的配体金纳米团簇被成功结晶,人们试图提出理论模型解释其结构稳定性,但并未获得普遍成功。上海应用物理研究所研究团队与美国内布拉斯加大学林肯分校和中国科技大学合作,建立了一个普适模型,实现了对迄今为止报道的所有71个配体金纳米团簇的基本理解。该模型认为每个金原子有三个不同的电子价态,三个或者四个金原子可以满足2电子的满壳层电子态,从而构成基本的结构单元(三角形Au3和四面体Au4)。当这些基本单元堆积在一起时,就形成了结构各异的稳定的金纳米团簇。该模型的建立,有力的证明了金纳米团簇的结构和生长遵循着基本的化学规律,从而为进一步理解金以外的金属纳米团簇打开了新的思路。由于这个模型非常类似于粒子物理中的基本粒子模型(即夸克有三个不同的“味”,三个夸克或者四个夸克构成核子,并进一步构成原子核和原子),所以被称为“全统一模型”(Grand Unified Model)。研究人员利用该模型预测了一系列高度稳定的金团簇,从而为实现基于化学规则的纳米金团簇可控合成提供了基础。相关研究成果发表在《自然-通讯》杂志上。(A grand unified model for liganded gold clusters, Nat. Commun. 7, 13574 doi: 10.1038/ncomms13574 (2016))。
计算化学领域:水纳米
领域介绍
水是生命之源,是这个星球上最常见的环境之一,但水环境对于固体纳米材料结构性质的影响并没有得到足够的重视。这一方面是由于人们普遍认为水环境对于固体材料的影响微乎其微可以忽略,另一方面是由于实验上观察水环境对固体结构影响的工作需要用到最先进的原位观测技术。因此,对此问题的理论研究就显得非常必要和迫切。
典型案例
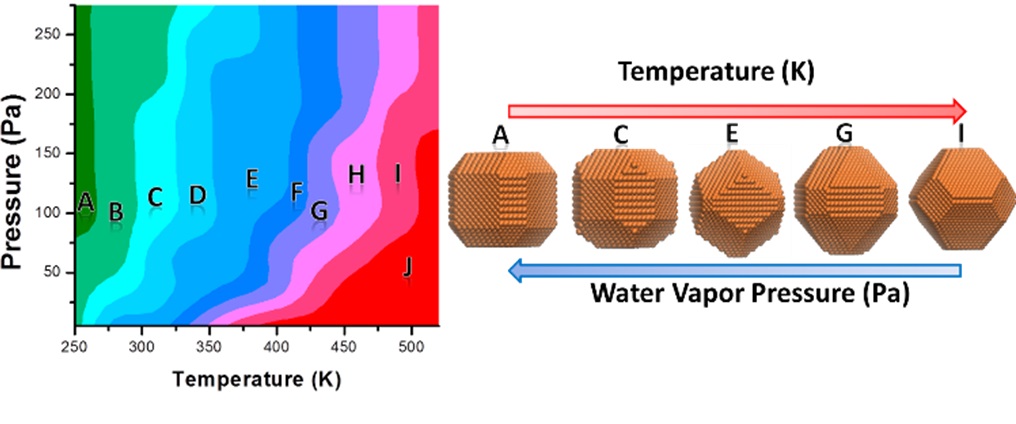
中国科学院上海应用物理研究所研究团队在传统的Wulff Construction理论的基础上,结合Langmuir分子吸附模型与第一性原理计算成功的将温度与水汽环境等多实验参量与金属稳定形貌联系了起来。借助于自主开发的多尺度模型和计算机模拟,成功观察到铜纳米颗粒在不同水汽环境中的稳定构型,并再现了实验结果。同时,他们对水汽环境中金、铂、钯等常用纳米催化剂的形貌进行了构建。这一工作不仅对纳米催化以及纳米材料学领域的实验学家能起到很好的理论指引作用,有助于人们正确认识水-固相互作用,同时为进一步研究介观尺度上外界环境对固体材料的影响提供了一个简单有效的理论模型。相关结果发表于《纳米快报》(Nano Letters 2016, 16, 2628-2632)。
计算力学领域:混沌动力系统模拟
典型案例
上海交通大学提出求解混沌动力系统一种新的数值计算策略——Clean Numerical Simulation(简称CNS),成功获得混沌动力系统较长时域内收敛的数值解。CNS是基于任意阶泰勒级数和任意精度(multiple precision)的浮点运算,同时降低截断误差和舍入误差至足够小,并与采用更小数值噪音所获得的数值结果进行收敛性和可靠性校验。2009年,廖世俊教授应用CNS首次获得 Lorenz 方程在[0,1000]LTU(Lorenz Time Unit)内收敛的数值模拟结果。2013年,采用国家超算天津中心TH-1A上的1200个CPUs和高效并行算法,廖世俊和王鹏飞(中国科学院)采用 3500 阶泰勒级数和 4180 位精度的数据首次得到Lorenz方程在时域 [0,10000] LTU 收敛的混沌解。
课题组应用CNS和国家超算天津中心TH-1A成功获得二维 Rayleigh-Bénard 对流收敛的数值结果,发现 Rayleigh-Bénard 对流中的湍流是可以自激产生的,揭示了微观尺度的热涨落是湍流随机性的起源。此外,廖世俊教授和李晓明博士应用CNS研究了混沌三体系统微观不确定性的传播,计算结果表明,混沌或许是连接微观不确定性和宏观随机性的桥梁。
三体问题是一个著名的经典问题,可追索至17世纪的牛顿。其中,三体问题的周期解具有重要的意义,一直得到学术界的重视。遗憾的是,自牛顿以后三百年仅发现三体问题少量周期解。2017年,廖世俊研究小组与他人合作,应用CNS成功获得著名的三体问题二千余个全新的周期解。该研究成果两次被New Scientist报道。
这些成功的应用,充分体现了CNS的有效性和潜力。由于混沌动力系统从微观到宏观都普遍存在。因此,混沌动力系统的精准数值模拟,具有重要的理论意义和实际应用价值。因此,CNS可望为科学界提供一个研究混沌动力系统全新的手段和工具。毫无疑问,CNS是建立在高性能计算机的快速发展之上。

图 微观尺度的热涨落是湍流随机性的起源
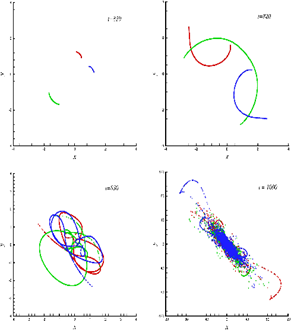
图 混沌三体问题的微观不确性的传播
